一些碎碎念
略微高估自己寒假在家的效率了
寒假打卡第一天共用时三天，因此本系列正式改名算法打卡第n期。
高精度
低位存个位，因为好向后拓展 auto 编译器推断自己的类型 ### 模版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21//高精度加法
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
// 判断长度
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55//高精度减法
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
//高精度乘法
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
//高精度除法
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
前缀和和差分
前缀和
定义
前缀和数组 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
using namespace std;
const int N=1e5+10;
int a[N];int s[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];\\求前缀和
for(int i=0;i<m;i++){
int l,r;
cin>>l>>r;
cout<<s[r]-s[l-1]<<'\n';
}
return 0;
}
1 | //一维前缀和 |
二维前缀和
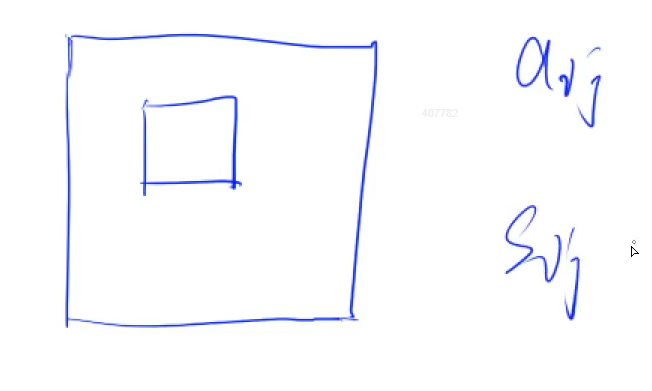Si,j是左上角所有元素的和
### 差分
#### 定义
是前缀和的逆运算,主要运用不是求差分运算，而是通过修改差分的值而算前缀和，从而达到降低时间复杂度的效果
####
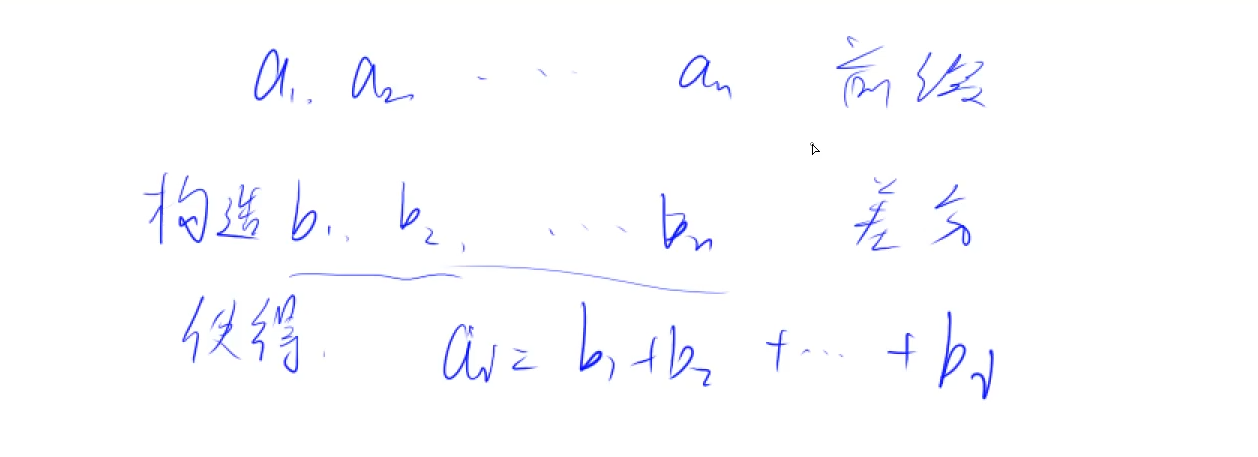一维差分
1 | //给区间[l, r]中的每个数加上c： |
二维差分
修改将Bi,j进行修改，会影响其右下角的值。 1
2 //给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
咕咕咕, 就快送到了
哎呀，似乎评论系统在您的地区都无法正常工作。
不过不要担心，来看看我们为您准备的备用方案 ——
1. 将您的评论用信封装好
2. 使用信鸽函至1476573945@qq.comexample.com
3. 我们在收到您的评论后将立即审核并更新至网站
评论一经采用，信函恕不退还，信鸽也不退还，请知悉。