- [[#每日任务:|每日任务:]]
- [[#快排|快排]]
- [[#快排#主要步骤|主要步骤]]
- [[#快排#几种做法|几种做法]]
- [[#几种做法#第一种|第一种]]
- [[#几种做法#第二种|第二种]]
- [[#快排#模版|模版]]
- [[#模版#模版题打卡|模版题打卡]]
- [[#快排#归并排序|归并排序]]
- [[#归并排序#模板|模板]]
- [[#归并排序#模板题打卡|模板题打卡]]
- [[#二分算法|二分算法]]
- [[#整数二分|整数二分]]
- [[#整数二分#适用范围|适用范围]]
- [[#整数二分#算法思路|算法思路]]
- [[#整数二分#模板|模板]]
- [[#整数二分#模板题打卡|模板题打卡]]
- [[#整数二分#浮点数二分|浮点数二分]]
# 一些碎碎念
从今天开始进行寒假算法集训QAQ,从数据结构学习完成之后就没有碰过C++,重新拿起来,还有一种比较陌生的感觉。顺带借此机会学习一下博客的搭建,尝试培养一下写博客的习惯,顺带接受网友们的监督,看看自己能够坚持几天(笑死 ### 每日任务: 题目
背板子
### 每日任务: 题目
背板子
排序
## 快排
基于分治算法 ### 主要步骤 1. 确定分界点: 2. 调整 区间:
比x小的在x左边,比x大的在x后面 3. 递归处理左右两边 ### 几种做法 ####
第一种 创建两个数组,后面再合并 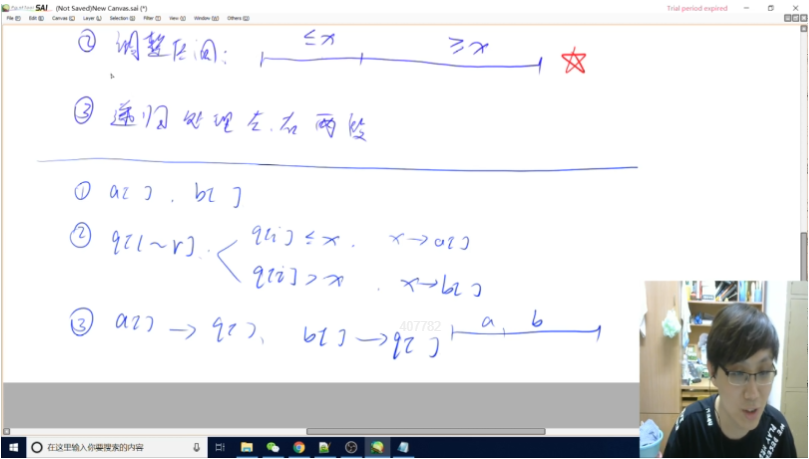 #### 第二种
两个指针同时向中间移动发现左右有都不满足的进行交换 ### 模版
#### 第二种
两个指针同时向中间移动发现左右有都不满足的进行交换 ### 模版
1
2
3
4
5
6
7
8
9
10
11
12
13
14void quick_sort(int q[], int l, int r)
{
if (l >= r) return;//如果左侧与右侧相遇即子串长为0递归结束
int i = l - 1, j = r + 1, x = q[l + r >> 1];//各退一位方便加减
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
//注意这边j千万 不能换成i,否则会出现边界错误
}
模版题打卡
 
归并排序
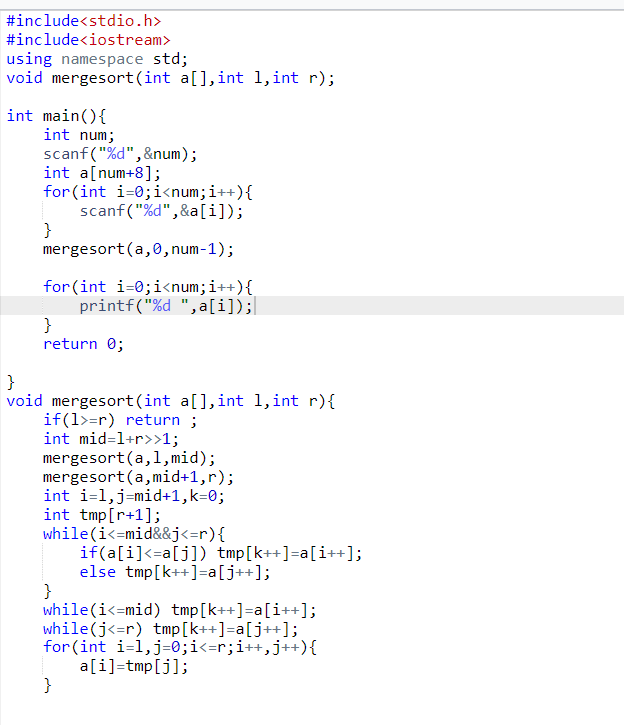
主要运用的也是分治思想 分为以下几步 1. 确定分界点mid=(l+r)/2 2. 递归排序 3. 合并
模板
1 | void merge_sort(int q[], int l, int r) |
模板题打卡
 ##
二分算法
##
二分算法
整数二分
适用范围
一种查找算法,用于在一段整体中前半部分和后半部分有一个可识别的状态,如下图,其中a部分满足条件,b部分不满足此条件。
.png) ### 算法思路
### 算法思路 .png) 注意:
取一号点时mid取值,为了是最后l与r相等,满足退出条件 ### 模板
注意:
取一号点时mid取值,为了是最后l与r相等,满足退出条件 ### 模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27bool check(int x) {/* ... */} // 检查x是否满足某种性质
//取1号点
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
//取2号点
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
模板题打卡
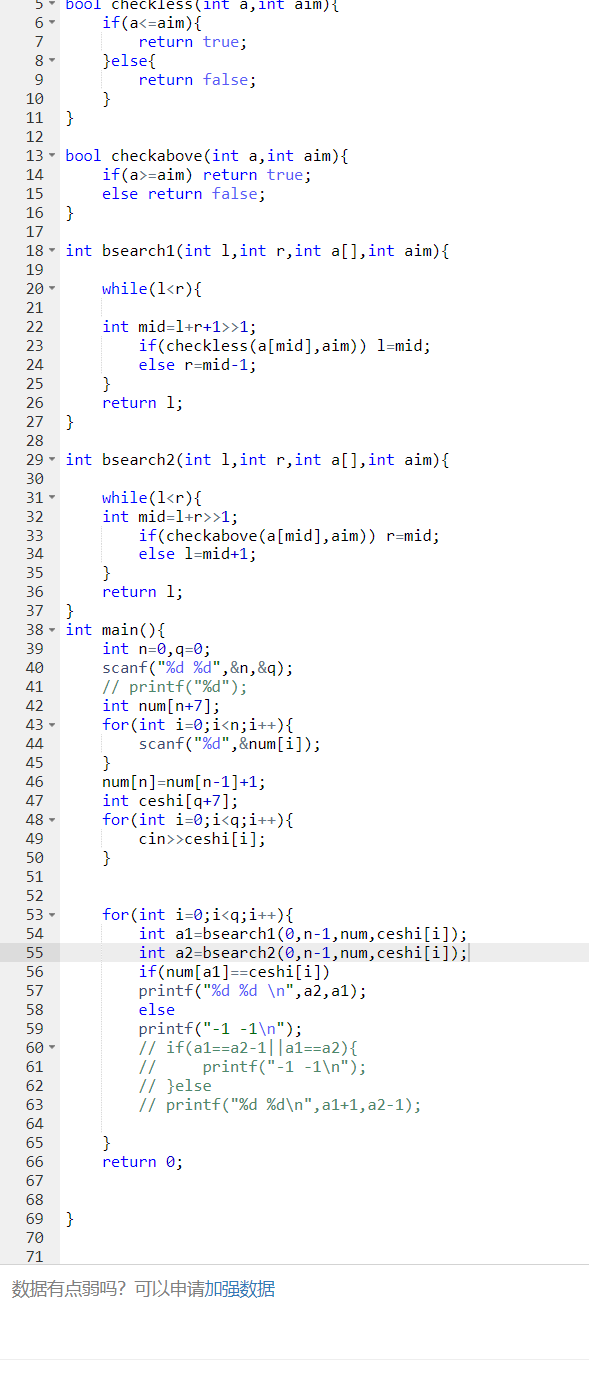 ### 浮点数二分
与整数二分相比,不需要考虑边界条件 如下题,求数的三次方根
### 浮点数二分
与整数二分相比,不需要考虑边界条件 如下题,求数的三次方根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
using namespace std;
int main(){
double l=-10000,r=100000;
double aim=0;
double mid=(l+r)/2;
cin>>aim;
while(abs(aim-mid*mid*mid)>=1e-9){
mid=(l+r)/2;
if (mid*mid*mid>aim) r=mid;
else l=mid;
}
printf("%.6lf",mid);
return 0;
}

咕咕咕, 就快送到了
哎呀,似乎评论系统在您的地区都无法正常工作。
不过不要担心,来看看我们为您准备的备用方案 ——
1. 将您的评论用信封装好
2. 使用信鸽函至1476573945@qq.comexample.com
3. 我们在收到您的评论后将立即审核并更新至网站
评论一经采用,信函恕不退还,信鸽也不退还,请知悉。